Trigonometry is the study of the sides and angles of triangles. Trigonometry can help us solve many real world problems.
Three basic formulas of right angle trigonometry are
sine, which is \[sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}\]
cosine, which is \[cos(\theta) = \frac{\text{adjacent}}{\text{hypotenuse}}\]
tangent, which is \[tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}\]
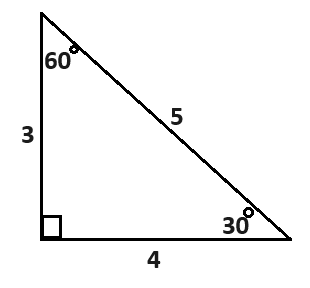
We need to label a triangle in order to use these formulas. The opposite and adjacent sides depend on which angle we are referencing.

If we reference 30 degrees in the above picture, then the opposite side is 3, as that is the side that is opposite of the angle 30 degrees. If, however, we reference 60 degrees, then 4 is the opposite side.
The hypotenuse side is always the side across from the right angle (the square in the bottom left corner is the right angle).
The adjacent side is always the side that is neither the opposite nor the hypotenuse. If we reference 30 degrees, then 4 is the adjacent side. If we reference 60 degrees, then 3 is the adjacent side.
A right angle trigonometry problem usually needs only one of these three formulas. You will choose which of the three formulas to use based on the triangle you are given. For example:
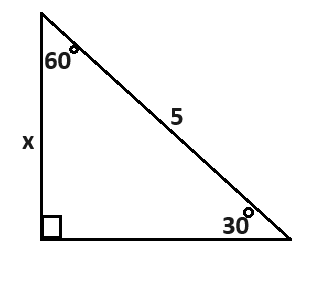
In the above picture, \(x\) is opposite of the 30 degree angle. We have the hypotenuse. We do not have the adjacent. We can only have one unknown value in the equation (which is \(x\)), so we will not use the trigonometric functions that include the adjacent side. That means sine is the function we want to use.
To solve for \(x\), we can substitute \(\theta = 30\), opposite = \(x\), and hypotenuse = \(5\) into the sine formula.
\[sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}\]
\[sin(30) = \frac{x}{5}\]
1.
A forester is helping a home owner assess the risk of a tree
falling on their home. The forester wants to estimate the height of the
tree. They measure and stand at a position that is 40 feet from the base
of the tree. They use a simple inclinometer to estimate the angle from
where they are standing to the top of the tree. The angle is 70 degrees.
How tall is the tree? (ignoring the height of the forester)
We can draw a triangle to represent the situation.
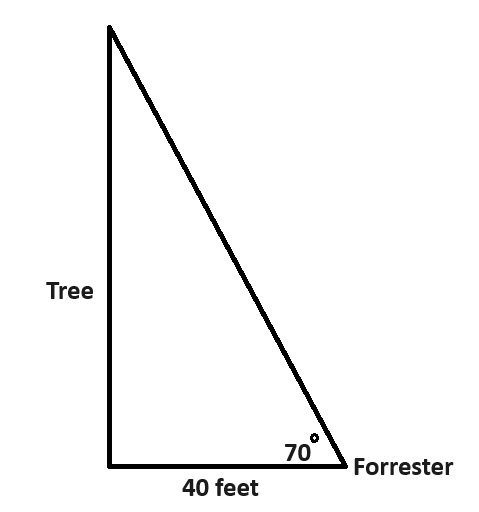
We want to solve for the height of the tree. The tree is opposite of the \(70\) degree angle. We do not know the hypotenuse side. We will not include the hypotenuse as our equation can only have one unknown. That means the remaining side of 40 feet is the adjacent side. The trigonometric function using opposite and adjacent is tangent.
\[tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}\]
We substitute \(\theta = 70\), \(\text{opposite } = \text{ tree}\), and \(\text{adjacent } = \text{ 40 feet}\) into the formula.
\[tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}\]
\[tan(70^{o}) = \frac{\text{tree}}{40}\]
We can evaluate \(tan(70^o)\) with a calculator. \(tan(70^o) \approx 2.747\)
\[tan(70^{o}) = \frac{\text{tree}}{40}\]
\[2.747 = \frac{\text{tree}}{40}\]
To get "tree" by itself, do the opposite to \(40\). Multiply \(40\) to both sides of the equation.
\[2.747 = \frac{\text{tree}}{40}\]
\[2.747 \cdot 40 = \frac{\text{tree}}{40} \cdot 40\]
\[109.88 = \text{tree}\]
The tree is approximately 110 feet tall. If the tree is within 110 feet of the house, it could be a concern!
2.
A ladder is supposed to be placed at a 75 degree angle (the 1 in 4
rule - one foot horizontally for every 4 vertical feet). A contractor
needs a ladder to reach 20 feet high on the house. Will a 20 foot ladder
work?
To make this determination, we can use right angle trigonometry. Here is a picture drawn for the scenario:
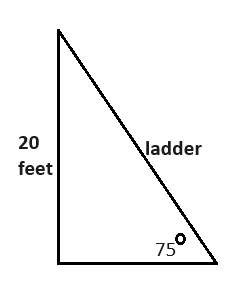
We want to solve for the side that is labeled "ladder". We can infer from the triangle that the ladder is the hypotenuse as the opposite angle appears to be a right angle. We have a 75 degree angle. We have the opposite side of 75 degrees (the 20 foot ladder). We need to solve for the hypotenuse. The trigonometric function that involves the opposite and hypotenuse is sine.
\[sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}\]
Substitute \(\theta = 75\) and opposite = 20 into the equation to solve.
\[sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}\]
\[sin(75) = \frac{20}{\text{hypotenuse}}\]
We can call the hypotenuse "x".
\[sin(75) = \frac{20}{x}\]
We cannot solve for \(x\) if it is in the denominator. Do the opposite of dividing by \(x\) to get \(x\) out of the denominator. Multiply both sides by \(x\).
\[sin(75) \cdot x = \frac{20}{x} \cdot x\]
\[sin(75) \cdot x = 20\]
We can evaluate \(sin(75)\) with a calculator.
\[sin(75) \cdot x = 20\]
\[0.96593 \cdot x = 20\]
Divide both sides by 0.96593 to get \(x\) by itself.
\[0.96593 \cdot x = 20\]
\[\frac{0.96593 \cdot x}{0.96593} = \frac{20}{0.96593}\]
\[x = 20.705\]
The length of the ladder needs to be roughly \(20.7\) feet, so a \(20\) foot ladder would probably be close enough.
1. A carpenter is working on the construction of a wooden roof. The roof’s framework includes a sloping beam that forms a 30-degree angle with the horizontal beam. The horizontal beam has a length of 12 feet. The carpenter needs to determine the length of the sloping beam. Calculate the length of the sloping beam.
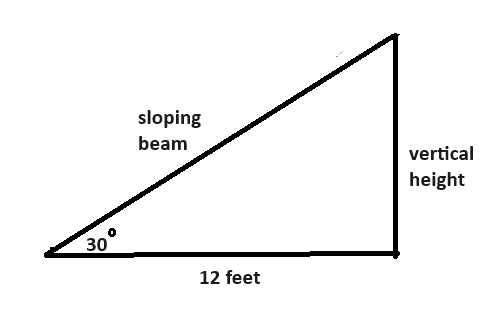
2. A surveyor needs to measure the distance across a river to determine the width of a piece of land on the opposite bank. The surveyor sets up their transit instrument on one side of the river and spots a point directly across the river on the opposite bank. They measure the angle of elevation to this point, which is 30 degrees. The surveyor knows the transit instrument is 4 feet above the ground. What is the horizontal distance across the river?
1. What other problems can you find where sine, cosine, or tangent would help to solve for a needed side?
2. What is the largest possible number that can result from plugging in an angle into \(sin(\theta)\)? From \(cos(\theta)\)? From \(tan(\theta)\)?