If we have a right triangle (one angle is 90 degrees), then we can use this formula:
\[a^2 + b^2 = c^2\]
where \(c\) is the hypotenuse of the triangle and \(a\) and \(b\) are the lengths of the other sides. The hypotenuse is always opposite of the right angle.
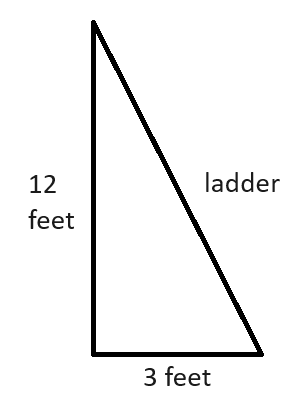
1. A rule of ladder safety is that a ladder should be 1 foot horizontally from a structure for every 4 feet vertically we want to reach. If a painter needs a ladder to reach 12 feet high on a home, how many feet must the ladder be?
If we need to reach 12 feet high, our ladder can be placed 3 feet horizontally away from the home. A triangle for the situation looks like this:

The ladder is the hypotenuse, as the ladder is opposite of the right angle. We can substitute \(a = 12\) and \(b = 3\) (or vice versa) into the Pythagorean theorem.
\[a^2 + b^2 = c^2\]
\[12^2 + 3^2 = c^2\]
\[144 + 9 = c^2\]
\[153 = c^2\]
\(c\) is currently being squared. To get rid of the square, we should square root both sides (we’ll ignore negative results).
\[153 = c^2\]
\[\sqrt{153} = \sqrt{c^2}\]
\[\sqrt{153} = c\]
or
\[12.369 \approx c\]
The ladder should be a little longer than 12 feet if possible.
2. A kayak is 12 feet long. A resident of Maine is thinking about purchasing one online, but they know that their shed is 10 feet deep and 6 feet high. If the resident puts the kayak diagonally like the picture shown, will it fit in the shed?
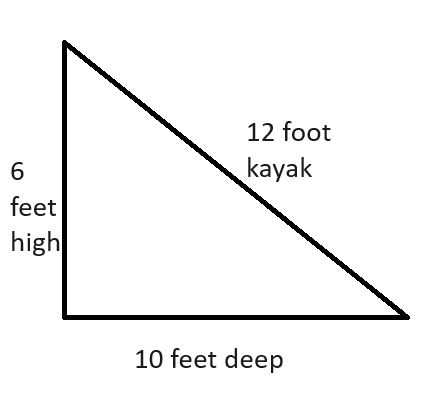
The triangle drawn might not be possible in real life. The 12 foot kayak might not be the correct value for the hypotenuse. To determine if it is, we can use the Pythagorean theorem to solve for the hypotenuse if the other two sides are \(6\) and \(10\).
\[6^2 + 10^2 = c^2\]
\[36 + 100 = c^2\]
\[136 = c^2\]
\[136 = c^2\]
\[\sqrt{136} = \sqrt{c^2}\]
\[11.6619 \approx c\]
It doesn’t look like the kayak would fit!
1. A carpenter needs to cut a piece of wood to match the length described below:
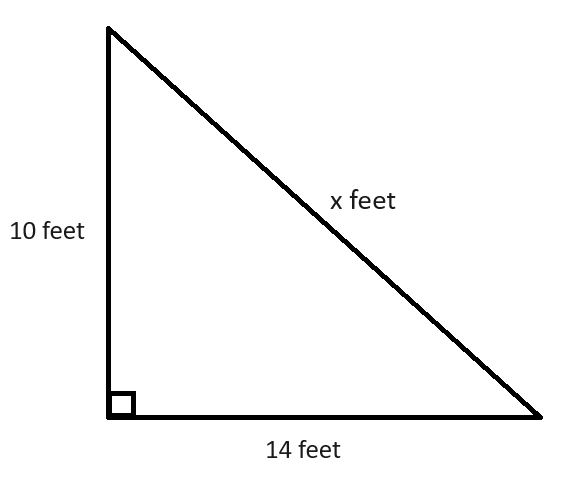
How long should the piece of wood labeled "x" be?
2. A person’s house is on a corner lot. They are building a fence, but due to town rules, they have to leave space so that their fence doesn’t block the sight of cars at an intersection. They have determined the fence will have the dimensions in the following picture:
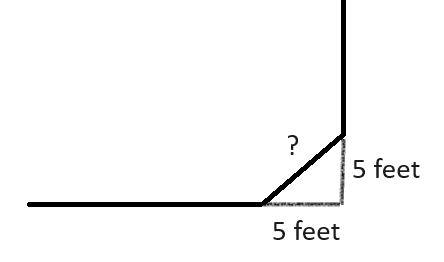
Find out how long the side with the ? must be.
1. What are some applications of the Pythagorean theorem that you can see in a trade you are interested in?
2. If our destination is 4 blocks east and 3 blocks west, what does the Pythagorean theorem tell us about the distance if we were to go instead diagonally to our destination (a straight route instead of two perpendicular turns)?