******* include logarithmic
We saw that some variables change by the same number over time. If a person is paid $15 an hour, then their pay changes by $15 every hour. We will now look at relationships where the amount of change goes up over time.
A common analogy of exponential change is the snowball analogy. If you start a small, sticky snowball at the top of the mountain, then roll it down the hill, the snowball gets a little bit bigger in the first few seconds, much bigger in the next few seconds, and then, suddenly, it’s out of control!
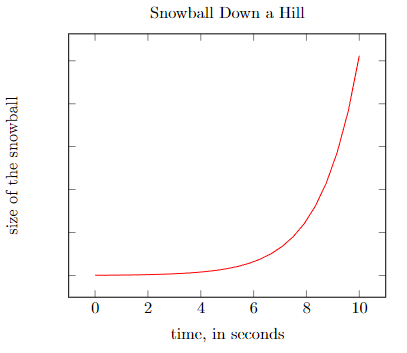
This is an example of an exponential rate of change. Exponential rates of change don’t always have to go up. They can go down.
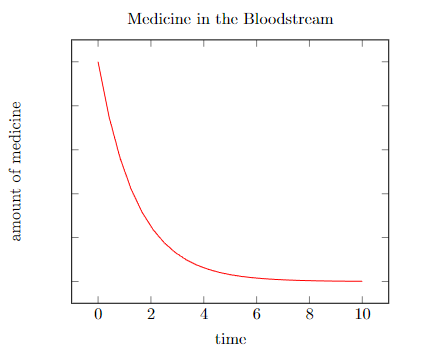
The amount of medicine in a bloodstream decreases rapidly at first due to the medicine being absorbed by the body.
Exponential functions have the following mathematical form (although the actual letters can be different):
\[a = b \cdot c^{d \cdot t}\]
You can think of a as the amount of medicine you have at time t, b as the starting amount of medicine, and c and d are numbers based on the particular person and the particular type of medicine.